What Is 2 3 Of 1 5
isesaas
Nov 30, 2025 · 8 min read
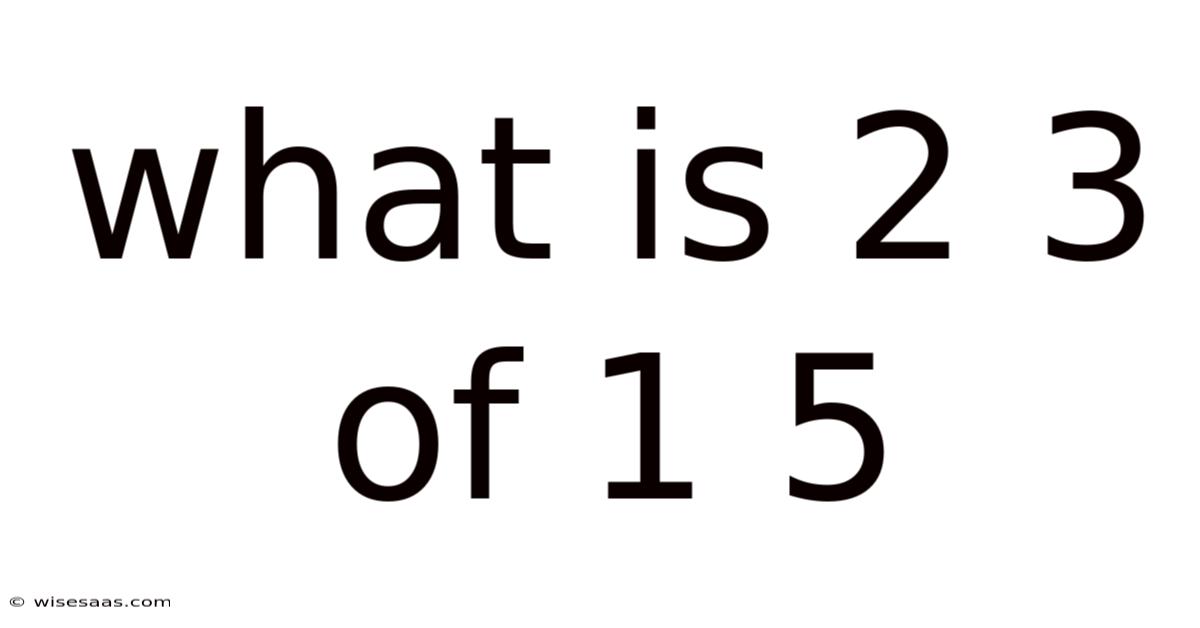
Table of Contents
Here's an in-depth explanation of how to calculate two-thirds of one-fifth, designed to be easily understood and informative. This article breaks down the concepts of fractions, multiplication, and provides practical examples to ensure clarity.
Understanding "What is 2/3 of 1/5?"
The question "What is 2/3 of 1/5?" is a mathematical problem that requires us to find a fraction of another fraction. In simpler terms, we want to determine what quantity we get when we take two-thirds (2/3) of one-fifth (1/5) of something. This type of problem is common in everyday situations such as dividing food, calculating portions, or understanding proportions in recipes. To solve it, we need to understand the basic concepts of fractions and multiplication.
Basic Concepts of Fractions
Before diving into the solution, let's briefly review what fractions are and how they work:
- Fraction: A fraction represents a part of a whole. It is written as a/b, where a is the numerator (the top number) and b is the denominator (the bottom number).
- Numerator: The numerator tells you how many parts of the whole you have.
- Denominator: The denominator tells you how many equal parts the whole is divided into.
For example, in the fraction 1/5, the whole is divided into 5 equal parts, and we have 1 of those parts. In the fraction 2/3, the whole is divided into 3 equal parts, and we have 2 of those parts.
Understanding "Of" in Mathematics
In mathematical terms, the word "of" often implies multiplication. When we say "2/3 of 1/5," we mean "2/3 multiplied by 1/5." This understanding is crucial because it transforms the word problem into a straightforward multiplication problem involving fractions.
Step-by-Step Solution to 2/3 of 1/5
Now that we understand the basic concepts, let's solve the problem step by step. To find 2/3 of 1/5, we need to multiply these two fractions together.
Step 1: Write down the fractions
Our fractions are 2/3 and 1/5.
Step 2: Multiply the numerators
Multiply the numerators (the top numbers) of the fractions:
2 x 1 = 2
Step 3: Multiply the denominators
Multiply the denominators (the bottom numbers) of the fractions:
3 x 5 = 15
Step 4: Write the resulting fraction
The result of multiplying the numerators becomes the new numerator, and the result of multiplying the denominators becomes the new denominator. Therefore, our new fraction is:
2/15
So, 2/3 of 1/5 is 2/15.
Detailed Explanation of Fraction Multiplication
To ensure complete understanding, let's delve deeper into why we multiply fractions in this way.
When we multiply fractions, we are essentially finding a fraction of a fraction. Consider a visual representation:
- Start with 1/5: Imagine a rectangle divided into 5 equal parts, and we shade 1 of those parts to represent 1/5.
- Take 2/3 of that 1/5: Now, we want to find two-thirds of that shaded 1/5. To do this, divide the shaded part into 3 equal sections and take 2 of those sections.
- Determine the new fraction: Count how many total sections there are in the whole rectangle (which is still divided into 5 parts horizontally). Then, consider how many of these sections represent the two-thirds of the one-fifth we initially shaded.
- Multiply: To find this mathematically, you multiply the numerators (2 x 1 = 2) to find out how many parts you now have and multiply the denominators (3 x 5 = 15) to determine the total number of parts in the whole.
This visual explanation helps to illustrate why multiplying the numerators and denominators gives us the correct answer.
Examples of Fraction Multiplication
To further solidify your understanding, let's look at a few more examples of multiplying fractions:
Example 1: What is 1/2 of 3/4?
- Multiply the numerators: 1 x 3 = 3
- Multiply the denominators: 2 x 4 = 8
- Result: 3/8
So, 1/2 of 3/4 is 3/8.
Example 2: What is 2/5 of 1/3?
- Multiply the numerators: 2 x 1 = 2
- Multiply the denominators: 5 x 3 = 15
- Result: 2/15
So, 2/5 of 1/3 is 2/15.
Example 3: What is 3/4 of 2/3?
- Multiply the numerators: 3 x 2 = 6
- Multiply the denominators: 4 x 3 = 12
- Result: 6/12
This fraction can be simplified to 1/2 by dividing both the numerator and denominator by 6. So, 3/4 of 2/3 is 1/2.
Simplifying Fractions
Sometimes, after multiplying fractions, you may end up with a fraction that can be simplified. Simplifying a fraction means reducing it to its lowest terms. To simplify a fraction, you need to find the greatest common divisor (GCD) of the numerator and the denominator and then divide both by the GCD.
For example, in the fraction 6/12 from Example 3 above, the GCD of 6 and 12 is 6. Dividing both the numerator and the denominator by 6 gives us 1/2, which is the simplest form of the fraction.
Real-World Applications
Understanding how to find a fraction of a fraction is useful in many real-world situations. Here are a few examples:
- Cooking: If a recipe calls for 1/2 cup of flour, but you only want to make 2/3 of the recipe, you need to find 2/3 of 1/2. This would be (2/3) x (1/2) = 2/6 = 1/3 cup of flour.
- Sharing Food: Suppose you have 1/4 of a pizza left, and you want to share 1/3 of that remaining pizza with a friend. You would calculate 1/3 of 1/4, which is (1/3) x (1/4) = 1/12. You would give your friend 1/12 of the whole pizza.
- Calculating Discounts: If an item is on sale for 1/2 off, and you have an additional coupon for 1/4 off the sale price, you need to calculate 1/4 of 1/2 to determine the additional discount. This would be (1/4) x (1/2) = 1/8.
Common Mistakes to Avoid
When multiplying fractions, there are a few common mistakes that students often make. Here are some to watch out for:
- Adding Instead of Multiplying: One common mistake is to add the numerators and denominators instead of multiplying them. Remember, when finding a fraction of a fraction, you should always multiply.
- Forgetting to Simplify: After multiplying, always check if the resulting fraction can be simplified. Simplifying fractions makes them easier to understand and work with.
- Incorrectly Identifying Numerators and Denominators: Make sure you know which number is the numerator (top) and which is the denominator (bottom). Mixing them up will lead to an incorrect answer.
- Not Understanding the "Of" Concept: Always remember that "of" in math problems usually means multiplication. This will help you correctly set up the problem.
Advanced Tips and Tricks
For those looking to deepen their understanding of fractions, here are a few advanced tips and tricks:
- Converting Mixed Numbers: If you are working with mixed numbers (e.g., 1 1/2), convert them to improper fractions before multiplying. For example, 1 1/2 becomes 3/2.
- Cross-Cancelling: Before multiplying, check if you can cross-cancel any common factors between the numerators and denominators. This can simplify the calculation. For example, in the problem 3/4 x 2/3, you can divide both 3s by 3 and both 2 and 4 by 2, resulting in 1/2 x 1/1 = 1/2.
- Estimating: Before calculating, estimate the answer to make sure your final result is reasonable. This can help you catch mistakes. For example, you know 2/3 is a little less than 1, and 1/5 is a small fraction, so 2/3 of 1/5 should be a small fraction as well.
Scientific Explanation of Fraction Multiplication
From a mathematical perspective, multiplying fractions is consistent with the properties of real numbers and the definition of multiplication as repeated addition. When we multiply two fractions, say a/b and c/d, we are essentially performing the operation:
(a/b) x (c/d) = (a x c) / (b x d)
This operation holds true because fractions are real numbers, and the multiplication of real numbers follows the associative and commutative properties. These properties ensure that the order in which we multiply numbers does not change the result, and that we can group numbers in any way we like without affecting the outcome.
Moreover, fraction multiplication is a fundamental operation in algebra and calculus. It is used in solving equations, simplifying expressions, and performing various mathematical analyses.
Conclusion
In conclusion, finding 2/3 of 1/5 is a straightforward multiplication problem that results in 2/15. By understanding the basic concepts of fractions, multiplication, and simplification, you can confidently solve similar problems in various contexts. Remember to always multiply the numerators and denominators, simplify the resulting fraction if possible, and apply these skills to real-world scenarios. With practice, you'll become more proficient in working with fractions and appreciate their practical applications in everyday life.
Latest Posts
Latest Posts
-
How Many Litres In 64 Ounces
Nov 30, 2025
-
How Many Feet Is 170 Cm
Nov 30, 2025
-
How Many Days Is 16 Weeks
Nov 30, 2025
-
What Is 21 Celsius In Fahrenheit
Nov 30, 2025
-
120 Km To Miles Per Hour
Nov 30, 2025
Related Post
Thank you for visiting our website which covers about What Is 2 3 Of 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.